完美信息博弈 vs 非完美信息博弈

• 完美信息博弈的例子：围棋，象棋。
• 非完美信息博弈的例子：德州扑克，麻将，有战争迷雾的游戏等。

两种博弈的理论最优解形式不同：

• 围棋局面的最优解是唯一的落点；
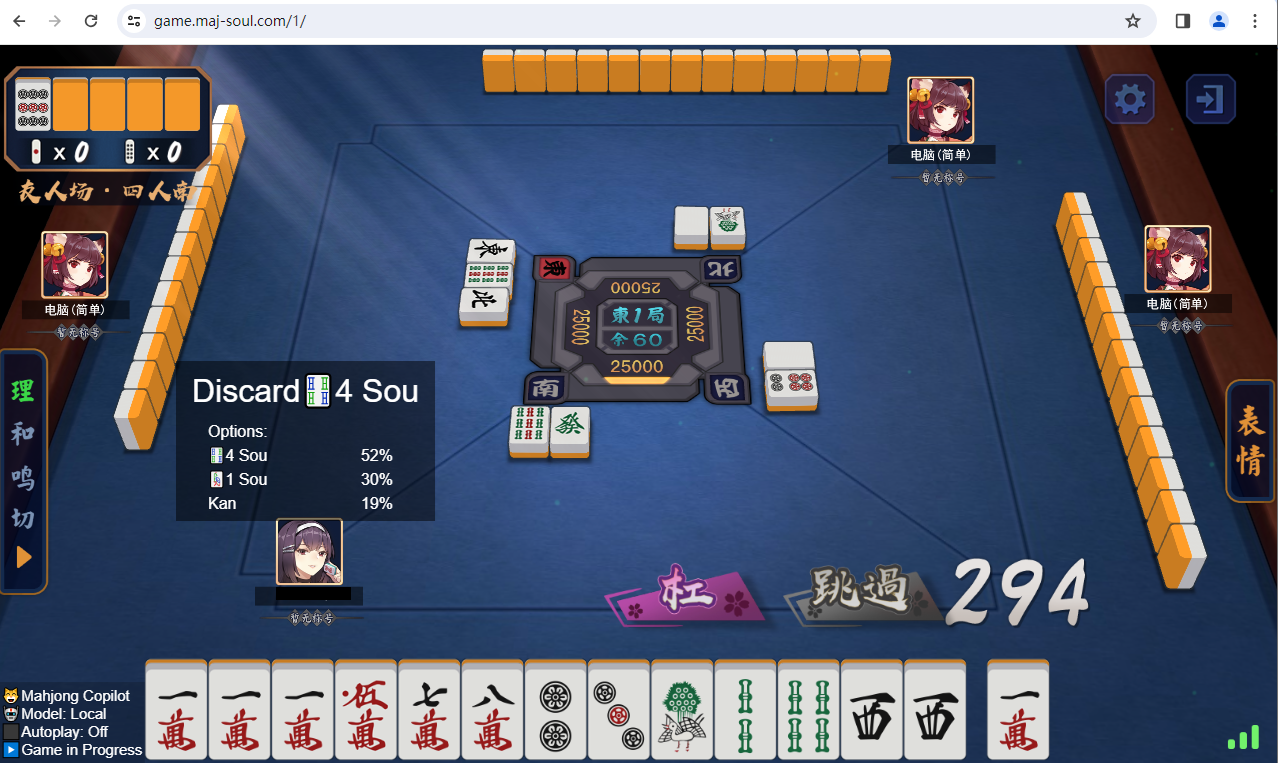
• 麻将局面的最优解是一个概率向量 (x%概率打A，y%概率打B，z%概率打C,…)，玩家根据概率随机选择行动。

一种直觉化的解释：德州扑克中，如果总是弃牌，或者总是 bluff，要不放弃很多正收益的局面，要不很容易被对手拆穿 bluff. 麻将中同理，如果只选概率最高的首选项，相当于简化成 (100%打A, 0%打B, 0%打C,…)，偏离了最优解。 因此，随机化的策略（去重）带来的结果，反而有可能更接近理论最优解。换句话说，适当随机化的策略，适应性更好，强度更高。

• 简化的例子1：多人多轮石头剪刀布对战。假设有统计资料表明，所有参加比赛的选手，出石头的概率最大。如果你的策略是，简单的每轮100%布，你的确会有超过50%的胜率，但你的策略适应性很差，会被针对。不仅被只出剪刀的简单策略针对，还会被更高级的，根据你出手历史动态调整的策略针对。所以，每轮的最优解一定是动态并且随机的，形似（50%布，30%石头，20%剪刀）。
• 简化的例子2：又如德州扑克，如果某策略每次碰到牌差就100%弃牌，就会错失一部分收益。所以，当池底筹码量很大，跟注额度又不高时，是不应完全放弃Bluff的。最优策略是形如（80%弃牌，18%跟牌，2%加注，…）